La Topología y la Geometría en la enseñanza educativa básica

Norma Leticia Cabrera Fermoso1, Rubén González Vera2, Herminia Mendoza Mendoza3 y Roberto Arzate Robledo4

Universidad Nacional Autónoma de México
FES Iztacala

Introducción

Actual­men­te, Méxi­co está vivien­do una trans­for­ma­ción edu­ca­ti­va por los sis­te­mas polí­ti­cos y guber­na­men­ta­les que exis­ten en el mun­do; con la glo­ba­li­za­ción se ha teni­do la nece­si­dad de imple­men­tar como estra­te­gia de estu­dio los mode­los de com­pe­ten­cias que exi­gen estu­dian­tes con cono­ci­mien­to poco pro­fun­do, pero espe­cia­lis­tas en des­tre­zas, lo que reper­cu­ti­do en la edu­ca­ción mexi­ca­na y en la ense­ñan­za (Barrón, 2005 y Ginés, 2004).

Con­si­de­ran­do que la edu­ca­ción vigen­te en Méxi­co es un tema de mucha impor­tan­cia, la SEP, en el “Mode­lo de Ges­tión Edu­ca­ti­va Estra­té­gi­ca” de 2001, mar­ca den­tro de sus linea­mien­tos la nece­si­dad de rea­li­zar inves­ti­ga­ción edu­ca­ti­va bási­ca para rein­cor­po­rar los datos obte­ni­dos en el mejo­ra­mien­to de la ense­ñan­za y obte­ner el míni­mo de deser­ción esco­lar en el nivel pri­ma­ria (Cabre­ra, 2012).

 En el pre­sen­te, la refor­ma edu­ca­ti­va de los pro­gra­mas y los méto­dos didác­ti­cos de la ense­ñan­za pri­ma­ria inten­ta lle­var a las aulas acti­vi­da­des de estu­dio que des­pier­ten el inte­rés de los alum­nos y los invi­ten a refle­xio­nar y a encon­trar dife­ren­tes for­mas de resol­ver pro­ble­mas. Con el estu­dio de las mate­má­ti­cas en la edu­ca­ción bási­ca se bus­ca que los niños y jóve­nes desa­rro­llen una for­ma de pen­sa­mien­to que les per­mi­ta inter­pre­tar y comu­ni­car cuan­ti­ta­ti­va­men­te situa­cio­nes que se pre­sen­tan en diver­sos entor­nos socio­cul­tu­ra­les. Téc­ni­cas ade­cua­das para reco­no­cer, plan­tear y resol­ver pro­ble­mas, gene­ran­do una acti­tud posi­ti­va hacia el estu­dio de esta dis­ci­pli­na, de cola­bo­ra­ción y crí­ti­ca, tan­to en el ámbi­to social y cul­tu­ral en que se desem­pe­ñen como en otros con­tex­tos.

Algu­nos pro­pó­si­tos que per­si­guen actual­men­te los estu­dios de las Mate­má­ti­cas en la Edu­ca­ción pri­ma­ria, son que los niños conoz­can y usen las pro­pie­da­des bási­cas de ángu­los y dife­ren­tes tipos de rec­tas, círcu­los, trián­gu­los, cua­drán­gu­los, polí­go­nos, pris­mas, pirá­mi­des, conos, cilin­dros y esfe­ras, al rea­li­zar algu­nas cons­truc­cio­nes y cal­cu­lar medi­das. Empleen y acla­ren diver­sos códi­gos sobre la orien­ta­ción en el espa­cio y ubi­car obje­tos y luga­res. Expre­sen y eva­lúen medi­das con dis­tin­tos tipos de uni­dad para con­je­tu­rar perí­me­tros y áreas de trián­gu­los, cua­dri­lá­te­ros y polí­go­nos regu­la­res e irre­gu­la­res. Pro­mue­van pro­ce­sos de bús­que­da, orga­ni­za­ción, aná­li­sis e inter­pre­ta­ción de datos con­te­ni­dos en imá­ge­nes, tex­tos, tablas y grá­fi­cas de barras para comu­ni­car infor­ma­ción o para res­pon­der pre­gun­tas plan­tea­das por sí mis­mos o por otros. Y sim­bo­li­cen infor­ma­ción median­te tablas y grá­fi­cas de barras. Iden­ti­fi­quen con­jun­tos de can­ti­da­des que varían o no pro­por­cio­nal­men­te, cal­cu­len valo­res fal­tan­tes y por­cen­ta­jes y apli­quen el fac­tor cons­tan­te de pro­por­cio­na­li­dad con núme­ros natu­ra­les en casos sen­ci­llos.

Estas acti­vi­da­des pre­ten­den orga­ni­zar los con­te­ni­dos de ense­ñan­za pri­ma­ria en tres ejes temá­ti­cos que coin­ci­den con los de nivel secun­da­ria: a) sen­ti­do numé­ri­co y pen­sa­mien­to alge­brai­co; b) for­ma, espa­cio y medi­da y c) mane­jo de infor­ma­ción. Inclu­yen­do tres aspec­tos esen­cia­les en los cua­les se basa el estu­dio de la geo­me­tría y la medi­ción: 1) Explo­ra­ción de las carac­te­rís­ti­cas y pro­pie­da­des de las figu­ras geo­mé­tri­cas. 2) Desa­rro­llo de las con­di­cio­nes nece­sa­rias para que ingre­sen en un tra­ba­jo carac­te­rís­ti­cas deduc­ti­vas. Y 3) Amplia­ción del cono­ci­mien­to de los prin­ci­pios bási­cos de ubi­ca­ción espa­cial y cálcu­lo geo­mé­tri­co: for­ma, espa­cio y medi­da.

Sin embar­go, aun cuan­do el con­te­ni­do de los pro­gra­mas edu­ca­ti­vos es espe­cí­fi­co y agru­pa una serie de cono­ci­mien­tos que deben ir desa­rro­llan­do los alum­nos, se ha encon­tra­do que gene­ral­men­te en los pri­me­ros nive­les no com­pren­den cómo emplear la geo­me­tría debi­do a la rigi­dez y abs­trac­ción de algu­nas nocio­nes y a la difi­cul­tad ter­mi­no­ló­gi­ca uti­li­za­da. Se ha obser­va­do que des­pués de obte­ner una serie de datos soli­ci­tán­do­les que los gra­fi­quen, no iden­ti­fi­can la grá­fi­ca con el dibu­jo de la situa­ción, sin poder com­pren­der una rela­ción de varia­bles. En el caso de nivel bási­co, se les pide la unión de dos o más pun­tos don­de los niños de eda­des más peque­ñas mues­tran no saber tra­zar o no enten­der para qué y por qué.

Cas­tro (2004) men­cio­na que los niños en sus pri­me­ros años de vida esco­lar se carac­te­ri­zan por una gran acti­vi­dad físi­ca, por la per­ma­nen­te inter­ac­ción que esta­ble­cen con su medio, por la cons­tan­te inves­ti­ga­ción que emer­ge de su intui­ción que los orien­ta a la bús­que­da de expli­ca­cio­nes median­te la cons­truc­ción y desa­rro­llo de su pen­sa­mien­to sim­bó­li­co y con­cre­to. El docen­te de los pri­me­ros años tie­ne bajo su res­pon­sa­bi­li­dad la selec­ción de acti­vi­da­des esco­la­res que favo­rez­can en los niños el cono­ci­mien­to geo­mé­tri­co y el desa­rro­llo de su capa­ci­dad de repre­sen­ta­ción.

Den­tro de estas acti­vi­da­des esco­la­res de repre­sen­ta­ción, el docen­te debe ir pro­mo­vien­do las nocio­nes topo­ló­gi­cas corres­pon­dien­tes (enten­dien­do a la topo­lo­gía como la orga­ni­za­ción per­cep­tual del espa­cio de los obje­tos en pro­xi­mi­dad, cer­ca­nía, sepa­ra­ción, orden, suce­sión espa­cial, inclu­sión, con­torno y con­ti­nui­dad, inde­pen­dien­te de la for­ma y el tama­ño de los cuer­pos,  que se logra a par­tir de la com­pren­sión de los mis­mos, median­te la acción), que le van a per­mi­tir a los niños ir cons­tru­yen­do reglas del espa­cio don­de se mue­ven, para pos­te­rior­men­te inte­grar­las a la geo­me­tría. Sin embar­go, son pocos los pro­fe­so­res preo­cu­pa­dos por iden­ti­fi­car que los alum­nos desa­rro­llen esta noción; y más crí­ti­co aún, es que los pro­gra­mas esco­la­ri­za­dos actua­les, no lo plan­teen.

El docen­te debe estar con­cien­te que hay una serie de ele­men­tos y rela­cio­nes geo­mé­tri­cas que no varían ante deter­mi­na­dos cam­bios como los esti­ra­mien­tos y los giros y que pre­ci­sa­men­te por esa inva­rian­cia los cono­ci­mien­tos geo­mé­tri­cos, son más acce­si­bles para los niños; por ejem­plo, si se hace un dibu­jo en un glo­bo, se infla y des­pués se suel­ta, habrá cosas del dibu­jo que cam­bia­rán, pero habrá cosas que no cam­bia­rán como un pun­to den­tro de una figu­ra o una línea con­ti­nua. Estas segun­das son las nocio­nes topo­ló­gi­cas, los con­jun­tos abier­tos en que están bien defi­ni­dos los con­tor­nos para cada uno de sus pun­tos. Asi­mis­mo, las fun­cio­nes con­ser­van los lími­tes, es decir, en la rela­ción de un con­jun­to dado X y otro con­jun­to de ele­men­tos Y, a cada ele­men­to X le corres­pon­de un úni­co ele­men­to. A pun­tos cer­ca­nos les corres­pon­den pun­tos cer­ca­nos, como por ejem­plo el cos­to de una lla­ma­da tele­fó­ni­ca que depen­de de su dura­ción.

El espa­cio topo­ló­gi­co se cons­tru­ye cuan­do se for­man estruc­tu­ras de cono­ci­mien­to basa­das en la inda­ga­ción de los obje­tos exter­nos que pro­por­cio­nan infor­ma­ción sobre patro­nes regu­la­res de fun­cio­na­mien­to seme­jan­tes para todos los ambien­tes; agru­pan­do en una sola uni­dad de cono­ci­mien­to la dis­tri­bu­ción de la infor­ma­ción dis­tin­ta que sur­ge de los sen­ti­dos y el ambien­te. El espa­cio topo­ló­gi­co posee seme­jan­za exter­na con los obje­tos com­pa­ra­dos, pues está deli­mi­ta­do, pero no deter­mi­na­do, ya que no posee ele­men­tos diso­cia­dos, sino que todos se encuen­tran en un con­glo­me­ra­do. Esto no impi­de que la men­te pue­da indu­cir dis­tin­tos órde­nes en la infor­ma­ción topo­ló­gi­ca y que el tipo de infor­ma­ción pre­do­mi­nan­te des­ta­que sobre los demás, pero tal pre­do­mi­nio no es una diso­cia­ción sino una glo­ba­li­za­ción con el res­to. No pre­sen­ta ele­men­tos pro­yec­ti­vos, como cen­tro de refe­ren­cia, orien­ta­ción con ori­gen común, pro­fun­di­dad y dis­tan­cia; ni geo­mé­tri­cos, como los sis­te­mas de refe­ren­cia, coor­de­na­das, esfé­ri­cos, cilín­dri­cos y lon­gi­tu­des, entre otros (Durán, Gómez y Mar­tí­nez, 2000).

Vidal y De la Torre, en 1984, en su artícu­lo Ense­ñan­za de la Topo­lo­gía y Geo­me­tría en los nive­les ele­men­ta­les, con­si­de­ra­ban que la Geo­me­tría no ha encon­tra­do un lugar ade­cua­do en la ense­ñan­za de las Mate­má­ti­cas y que la des­apa­ri­ción gra­dual de ésta en los pro­gra­mas edu­ca­ti­vos pri­ma­rios es alar­man­te. Que aún cuan­do los con­te­ni­dos de los pro­gra­mas de ense­ñan­za pri­ma­ria eran ambi­cio­sos en cuan­to a lo que el alumno debe apren­der en Mate­má­ti­cas, no iden­ti­fi­ca­ban en éstos el desa­rro­llo de la Topo­lo­gía como géne­sis para la com­pren­sión y refle­xión de la Geo­me­tría.

Men­cio­nan que “en cada nivel de desa­rro­llo cog­nos­ci­ti­vo —esco­lar o no— hay una Geo­me­tría que se apren­de por sí mis­ma, siem­pre que se le dé la opor­tu­ni­dad de desa­rro­llar­se, y que es un com­po­nen­te esen­cial de este desa­rro­llo” (p.2) refi­rién­do­se a la topo­lo­gía. Y que el desa­rro­llo de ésta se pue­de obser­var en los jue­gos infan­ti­les de los niños, pri­me­ra­men­te, de una mane­ra dis­per­sa pero con­for­me accio­nan los obje­tos, logran des­cu­brir las rela­cio­nes exis­ten­tes que median­te ejer­ci­ta­ción las trans­for­man en leyes geo­mé­tri­cas.

Por su par­te, Postijo y cols. (2007) refie­ren que la topo­lo­gía ha sido un tema poco estu­dia­do y que su desa­rro­llo per­mi­te la evo­lu­ción de la inte­li­gen­cia lógi­co- mate­má­ti­ca; que a par­tir de los 7 años el niño ha desa­rro­lla­do esta noción y está lis­to para las mate­má­ti­cas; al com­pa­rar dos con­jun­tos, el niño de 6 o 7 años ya pue­de con­tar el núme­ro de can­ti­da­des; pri­me­ro, com­pa­ra las can­ti­da­des tota­les de cada con­jun­to y pos­te­rior­men­te deter­mi­na la exten­sión espa­cial con la can­ti­dad.

Cas­tro (2004) seña­la al res­pec­to que la ense­ñan­za de los con­cep­tos mate­má­ti­cos tra­di­cio­nal­men­te ha que­da­do res­trin­gi­da exclu­si­va­men­te a expe­rien­cias de carác­ter eucli­diano (posi­ción, pro­por­ción y dis­tan­cia), inte­grán­do­se en ésta los aspec­tos pro­yec­ti­cos (espa­cio y pro­fun­di­dad) y topo­ló­gi­cos (la unión de dos o más con­jun­tos en un espa­cio), los cua­les deben ser desa­rro­lla­dos de mane­ra y en rela­ción inde­pen­dien­te. Asi­mis­mo, que es muy impor­tan­te que los docen­tes, prin­ci­pal­men­te los que atien­den los pri­me­ros nive­les de edu­ca­ción, conoz­can cómo se desa­rro­lla la topo­lo­gía y cómo se inte­gra con la geo­me­tría.

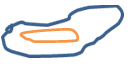
Con­ti­núa seña­lan­do que la topo­lo­gía son las expe­rien­cias mate­má­ti­cas que va tenien­do el niño, expre­sa­das median­te la repre­sen­ta­ción grá­fi­ca (dibu­jo) del acer­ca­mien­to, sepa­ra­ción, orden, entorno y con­ti­nui­dad de los obje­tos (figu­ra 1).

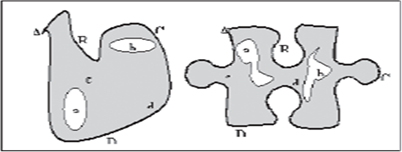
Figura 1. Desarrollo Topológico

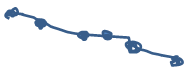
En este tipo de repre­sen­ta­ción grá­fi­ca, pue­den exis­tir trans­for­ma­cio­nes de la figu­ra ori­gi­nal, que pue­den ser tan pro­fun­das y gene­ra­les, que alte­ren los ángu­los, las lon­gi­tu­des, las rec­tas, las áreas, los volú­me­nes, los pun­tos y las pro­por­cio­nes.

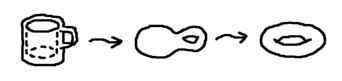
Figura 2. Transformación Topológica

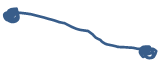
No obs­tan­te, a pesar de las tras­for­ma­cio­nes algu­nas rela­cio­nes o pro­pie­da­des geo­mé­tri­cas per­ma­ne­cen inva­ria­bles.

Figura 3. Propiedades Invariables en el Desarrollo de la Topología.

Este mis­mo autor indi­ca, que el desa­rro­llo de la topo­lo­gía está uni­do al desa­rro­llo de la noción de espa­cio y gene­ral­men­te cobra fuer­za cuan­do el niño pue­de des­pla­zar­se y coor­di­nar sus accio­nes. La noción de espa­cio se va desa­rro­llan­do a la par de la con­ser­va­ción del obje­to, sin embar­go, en oca­sio­nes pue­de pre­sen­tar difi­cul­ta­des deri­va­das de lagu­nas de cono­ci­mien­to crea­das por la edu­ca­ción. Tra­di­cio­nal­men­te, se ha hecho énfa­sis en la ense­ñan­za de la Geo­me­tría Eucli­dia­na y se des­cui­dan los otros dos aspec­tos del espa­cio total: el Topo­ló­gi­co y el Pro­yec­ti­vo.

En 1980, Maj­luf desa­rro­lló dos esca­las para eva­luar la posi­ción y la pers­pec­ti­va del dibu­jo espon­tá­neo en los niños de 6 a 8 años, basán­do­se en la teo­ría pia­ge­tia­na res­pec­to a la orga­ni­za­ción jerár­qui­ca de las rela­cio­nes espa­cia­les, que esta­ble­ce que el desa­rro­llo de la habi­li­dad para dibu­jar es para­le­la a la capa­ci­dad para orga­ni­zar el espa­cio y la for­ma­ción del pen­sa­mien­to ope­ra­to­rio. Encon­tran­do que el cre­ci­mien­to topo­ló­gi­co se pue­de obser­var a par­tir de los 4 años en el dibu­jo. Los resul­ta­dos de su inves­ti­ga­ción per­mi­ten con­cluir que sería jus­ti­fi­ca­ble con­ti­nuar ana­li­zan­do la inter­re­la­ción entre la habi­li­dad para dibu­jar y la cons­truc­ción de con­cep­tos espa­cia­les y cog­ni­ti­vos en niños de mayor edad.

Para Pia­get y Gar­cía (1998) y Mar­tí (2000), la noción de espa­cio se cons­tru­ye pau­la­ti­na­men­te siguien­do el orden que par­te de las expe­rien­cias: Topo­ló­gi­cas, Pro­yec­ti­vas y Eucli­dia­nas, con­tra­rio al orden en que his­tó­ri­ca­men­te fue­ron for­ma­li­za­das las res­pec­ti­vas geo­me­trías. En una pri­me­ra eta­pa, el espa­cio está redu­ci­do al movi­mien­to sen­so­rio­mo­tor del niño (espa­cio per­cep­tual) y tie­ne como mar­co al cuer­po como cen­tro prin­ci­pal y de refe­ren­cia. Al final de esta eta­pa el niño per­ci­be las rela­cio­nes espa­cia­les entre las cosas, pero no las repre­sen­ta toda­vía en ausen­cia de con­tac­to direc­to.

A la edad de dos años apro­xi­ma­da­men­te, el niño va for­man­do la noción de espa­cio a tra­vés del cono­ci­mien­to de: arri­ba, aba­jo, enci­ma, atrás, que se va favo­re­cien­do con el desa­rro­llo topo­ló­gi­co (pro­xi­mi­dad, orden, con­ti­nui­dad). “En esta eta­pa el niño no pue­de dis­tin­guir un círcu­lo de un cua­dra­do por­que ambas son figu­ras cerra­das, pero si las pue­de dife­ren­ciar de la figu­ra de una herra­du­ra. Pos­te­rior­men­te logra dis­tin­guir líneas cur­vas de rec­tas y figu­ras lar­gas de cor­tas, así como tam­bién dife­ren­ciar el espa­cio inte­rior y exte­rior de una fron­te­ra dada o deter­mi­nar posi­cio­nes rela­ti­vas al inte­rior de un orden lineal” (Cas­tro, 2004, p.6).

En esta eta­pa el niño va ela­bo­ran­do las repre­sen­ta­cio­nes men­ta­les que le van a per­mi­tir la cons­truc­ción del cono­ci­mien­to mate­má­ti­co. Sin embar­go, si el niño no ha esta­ble­ci­do la noción de con­ser­va­ción de núme­ro, masa y volu­men, ten­drá difi­cul­ta­des, para desa­rro­llar la noción de espa­cio.

Según Pia­get (en: Carra­ta­lá, 1985) a par­tir de los seis años los con­cep­tos topo­ló­gi­cos se empie­zan a trans­for­mar en con­cep­tos pro­yec­ti­vos y con­cep­tos eucli­dia­nos, per­mi­tién­do­le al niño la cons­truc­ción de un espa­cio exte­rior, ela­bo­ran­do repre­sen­ta­cio­nes men­ta­les para ubi­car­se des­de otro pun­to de vis­ta; con lo que podría dibu­jar una casa de enfren­te en la que se tras­pa­ren­ta el inte­rior. En esta eta­pa las rela­cio­nes topo­ló­gi­cas se apli­can a todas las for­mas y las rela­cio­nes eucli­dia­nas y pro­yec­ti­vas comien­zan a emer­ger; en ese momen­to ya per­ci­be los obje­tos no como algo está­ti­co sino como obje­tos con movi­mien­to. El espa­cio pro­yec­ti­vo sur­ge cuan­do un obje­to lle­ga a ser con­si­de­ra­do men­tal­men­te en rela­ción a un pun­to de vis­ta; el niño comien­za enton­ces a apre­ciar cómo se pre­sen­tan los obje­tos cuan­do son con­tem­pla­dos des­de dife­ren­tes posi­cio­nes.

Por tan­to, la base de las mate­má­ti­cas, según Pia­get (1999), se encuen­tra en el pro­ce­so refle­xi­vo que el niño hace cuan­do accio­na los obje­tos en su entorno. Las acti­vi­da­des que rea­li­za en edad pre­es­co­lar y que se refie­ren a la noción de espa­cio, son fun­da­men­tal­men­te expe­rien­cias de carác­ter topo­ló­gi­co (orde­nar, agru­par, amon­to­nar, doblar, esti­rar, pegar, colo­rear, com­ple­tar, recor­tar, hacer corres­pon­der, posi­cio­nar y des­pla­zar, entre otras); no obs­tan­te, esto no exclu­ye la posi­bi­li­dad de que en la eta­pa de edu­ca­ción ini­cial, inter­pre­te y com­pren­da algu­nas expe­rien­cias, de tipo pro­yec­ti­vo y eucli­diano, al menos, en sus pri­me­ras apro­xi­ma­cio­nes. De ahí la impor­tan­cia de su estu­dio y su inves­ti­ga­ción.

Por últi­mo, cabe des­cri­bir que Postijo y cols. (2007), rea­li­za­ron una inves­ti­ga­ción que tenía como obje­ti­vo, deter­mi­nar el gra­do de efec­ti­vi­dad de la apli­ca­ción de la topo­lo­gía, en el desa­rro­llo de la inte­li­gen­cia lógi­co mate­má­ti­ca. Para tal efec­to, uti­li­za­ron 24 alum­nos del pri­mer gra­do de edu­ca­ción pri­ma­ria del Cole­gio Nacio­nal Her­mi­lio Val­di­za­na. El méto­do emplea­do fue el méto­do his­tó­ri­co de tipo expe­ri­men­tal, usan­do ins­tru­men­tos didác­ti­cos como blo­ques lógi­cos, lápi­ces de colo­res y una entre­vis­ta, para obte­ner infor­ma­ción de cam­po, en la pobla­ción estu­dia­da. Encon­tran­do que el ejer­ci­cio de diver­sos aspec­tos de la topo­lo­gía (for­ma y figu­ra) en los niños, opti­mi­za su pro­ce­so de con­cre­ción abs­trac­ción y for­ma­li­za­ción, faci­li­tan­do la cons­truc­ción de la inte­li­gen­cia lógi­co-mate­má­ti­ca, hallaz­go con­gruen­te con los pos­tu­la­dos de Jean Pia­get. Ade­más de ubi­car las estra­te­gias que usan los niños en el desa­rro­llo del len­gua­je geo­mé­tri­co a par­tir de la apli­ca­ción de ésta área for­mal. Con­clu­yen­do que el avan­ce de las nocio­nes topo­ló­gi­cas favo­re­ce la madu­rez men­tal y cog­ni­ti­va de la inte­li­gen­cia.

En con­cre­to, como pro­pues­ta didác­ti­ca, se pue­de seña­lar que exis­ten dis­tin­tas acti­vi­da­des que los docen­tes de edu­ca­ción pre­es­co­lar pue­den rea­li­zar para for­ta­le­cer el desa­rro­llo topo­ló­gi­co y que se refie­ren a la noción de espa­cio que brin­dan la posi­bi­li­dad de con­so­li­dar a lar­go pla­zo las bases de la com­pren­sión de la noción de espa­cio total: orde­nar, agru­par, amon­to­nar, doblar, esti­rar, pegar, colo­rear, com­ple­tar, recor­tar, hacer corres­pon­der, posi­cio­nar y  des­pla­zar, como casos que faci­li­tan la cons­ti­tu­ción de una geo­me­tría del obje­to res­pec­to a un espa­cio, tal como se mues­tra en la figu­ra 4. Este ejer­ci­cio no exclu­ye la posi­bi­li­dad de que el niño pue­da inter­pre­tar y com­pren­der algu­nas expe­rien­cias de tipo pro­yec­ti­vo y eucli­diano, al menos en sus pri­me­ras apro­xi­ma­cio­nes.

Exploración educativa del docente con el niño, en las siguientes experiencias, de desarrollo Topológico:

Abier­to  Cerra­do	Una línea es abier­ta si tie­ne dos extre­mos. Una Línea es cerra­da si no tie­ne extre­mos
Sim­ple Com­ple­ja	Una línea es sim­ple si no tie­ne nudo. Una línea es com­ple­ja si los tie­ne
Con­ti­nua Dis­con­ti­nua	Una línea es con­ti­nua si se pue­de reco­rrer sin levan­tar el lápiz. Es dis­con­ti­nua si hay peque­ños brin­cos
Den­tro Fue­ra	Línea cerra­da que deli­mi­ta un pun­to del espa­cio externo.  Pun­to que se encuen­tra fue­ra de la fron­te­ra de la línea cerra­da.
Cone­xo	Una figu­ra es cone­xa si se pue­de reco­rrer varias veces el mis­mo pun­to sin salir­se de ella.
Inco­ne­xa	Es inco­ne­xa la figu­ra, si se encuen­tra divi­di­da en varios tro­zos.
Sim­ple cone­xo	Si den­tro de la figu­ra no tie­ne hue­cos.
No sim­ple cone­xo	Si den­tro de la figu­ra tie­ne hue­cos.
Vecino	Dos pun­tos son veci­nos, si en medio no exis­te otro.
Extre­mos	Un ele­men­to de una línea es extre­mo si tie­ne un sólo vecino.

Figura 4. Desarrollo topológico que los niños en edad preescolar deben desarrollar, fundamentado en la literatura psicológica general, sobre topología, en edades preescolares y escolares.

Para lle­var a cabo el desa­rro­llo topo­ló­gi­co corres­pon­dien­te en la edad pre­es­co­lar se reco­mien­da de modo gene­ral como guía didác­ti­ca las siguien­tes acti­vi­da­des:

Desarrollo topológico en edad preescolar

Par­ti­ci­pan­tes: Niños de pre­es­co­lar entre 4 y 5 años de edad, apro­xi­ma­da­men­te.

Esce­na­rio: Las acti­vi­da­des se deben rea­li­zar en el salón don­de gene­ral­men­te reci­ben cla­ses los niños.

Mate­rial: Ligas de plás­ti­co de colo­res, estam­bre, plas­ti­li­na, papel de chi­na, hojas de papel, palos de colo­res y cra­yo­las.

Meto­do­lo­gía:

Ins­tru­men­to: Méto­do clí­ni­co pia­ge­tiano.

Pro­ce­di­mien­to:

Colo­can­do a 4 y 5 niños en mesas cir­cu­la­res en el salón de cla­ses, se les pro­por­cio­na­rán ligas fle­xi­bles de colo­res para tra­ba­jar la trans­for­ma­ción topo­ló­gi­ca de líneas cerra­das. Duran­te 20 minu­tos se les per­mi­ti­rá jugar libre­men­te con las ligas para que accio­nen con ellas, que pue­dan dar­se cuen­ta de su fle­xi­bi­li­dad, tex­tu­ra, mate­rial y for­ma. Una vez rea­li­za­do, la maes­tra se para­rá enfren­te y les pedi­rá que esti­ren las ligas lado a lado, las regre­sa­rán a su lugar y les pedi­rá que las esti­ren a lo ancho, regre­san­do al pun­to ori­gi­nal y, por últi­mo, que las esti­ren de las esqui­nas.  En una hora los niños esta­rán ejer­ci­tan­do con la liga las nocio­nes de lar­go, ancho y esqui­nas. Al tér­mino de los ejer­ci­cios se les cues­tio­na­rá bajo los siguien­tes ejes: ¿Cuál es inte­rior de la línea y cuál es el exte­rior?

 Estos ejer­ci­cios lo rea­li­za­rán apro­xi­ma­da­men­te por quin­ce días. Una vez trans­cu­rri­do este tiem­po se pro­ce­de­rá a rea­li­zar los mis­mos ejer­ci­cios con papel de chi­na, duran­te otros quin­ce días. Pos­te­rior­men­te, cam­bia­rán a plas­ti­li­na por quin­ce días, y por últi­mo, con estam­bre grue­so. Des­pués de cada ejer­ci­cio, se les cues­tio­na­rá a los niños bajo el méto­do clí­ni­co, con los siguien­tes ejes: ¿Cuá­les son los pun­tos que unen a la línea? ¿Y por qué los une? En el ter­cer mes, se les dará duran­te quin­ce días con­se­cu­ti­vos labe­rin­tos dise­ña­dos pre­via­men­te por la maes­tra, para que los niños unan dos pun­tos con lápi­ces de colo­res. Al tér­mino se les cues­tio­na­rá a par­tir de dos ejes: ¿Cuá­les son los pun­tos que unen a la línea? ¿Y de qué modo se unen?

Duran­te los quin­ce días res­tan­tes del mes recor­ta­rán for­mas y figu­ras, pre­via­men­te dise­ña­das por la maes­tra y las pega­rán en car­tu­li­na blan­ca, don­de se encon­tra­rá de ante­mano la for­ma de la figu­ra.

En el cuar­to mes com­ple­to arma­rán rom­pe­ca­be­zas de 5 a 8 figu­ras. Al tér­mino se les cues­tio­na­rá median­te el méto­do clí­ni­co: ¿Cómo se jun­tan las figu­ras que for­man el rom­pe­ca­be­zas? y ¿de qué modo las unie­ron?  Por últi­mo, en el quin­to mes com­ple­to el ins­truc­tor impri­mi­rá en hojas de papel blan­co dis­tin­tos pun­tos con cra­yo­las, a lo lar­go de toda la hoja, y pos­te­rior­men­te les pedi­rá a los niños que los unan, has­ta for­mar varios dibu­jos.

Una vez prac­ti­ca­do, sabien­do que los niños en esta edad, nece­si­tan estar en pre­sen­cia del obje­to, para poder repre­sen­tar­lo, podrán tomar sólo una par­te del obje­to como índi­ce de su repre­sen­ta­ción, que les per­mi­ta la recons­truc­ción men­tal del obje­to, para poder evo­car­lo, en su ausen­cia y a tra­vés del tiem­po.

Por últi­mo, se reco­mien­da rea­li­zar las mis­mas acti­vi­da­des, toman­do como base algu­nas de las dife­ren­tes for­mas topo­ló­gi­cas, mar­ca­das en la figu­ra 1–4.

Desarrollo topológico en edad escolar

Alre­de­dor de los seis años apro­xi­ma­da­men­te, el niño ingre­sa al nivel de esco­la­ri­dad for­mal, don­de los con­cep­tos topo­ló­gi­cos comien­zan a trans­for­mar para él en con­cep­tos pro­yec­ti­vos que le impli­can la cons­truc­ción de una geo­me­tría del espa­cio exte­rior; la des­cen­tra­ción le per­mi­te esta­ble­cer la repre­sen­ta­ción de su espa­cio cir­cun­dan­te en la que los ejes ade­lan­te-atrás, izquier­da-dere­cha dejan de ser abso­lu­tos; es decir, van sien­do coor­di­na­dos en la medi­da en que efec­túa ope­ra­cio­nes men­ta­les que le posi­bi­li­tan  ver los obje­tos des­de otro pun­to de vis­ta.  Las trans­for­ma­cio­nes pro­yec­ti­vas con­du­cen al niño a visua­li­zar los cam­bios que sufren ángu­los y lon­gi­tu­des en la repre­sen­ta­ción del obje­to obser­va­do.

Par­ti­ci­pan­tes: Niños esco­la­res de 6 años de edad, apro­xi­ma­da­men­te.

Esce­na­rio: Las acti­vi­da­des se deben rea­li­zar en el salón, don­de gene­ral­men­te, reci­ben cla­ses.

Mate­rial: hojas blan­cas de papel, palos de colo­res, cra­yo­las.

Meto­do­lo­gía: Méto­do clí­ni­co pia­ge­tiano.

 Pro­ce­di­mien­to:

Algu­nas de las acti­vi­da­des que auxi­lia­rán el desa­rro­llo topo­ló­gi­co en esta edad son las siguien­tes: Soli­ci­tar que dibu­jen un pai­sa­je con los árbo­les cada vez más peque­ños; este tipo de acti­vi­dad les refle­ja­rá la pro­fun­di­dad y el ale­ja­mien­to median­te los cam­bios en las lon­gi­tu­des y los ángu­los que con­tie­ne; mien­tras que las líneas, pun­tos y pro­por­cio­nes, per­ma­ne­ce­rán inva­ria­bles.  Que median­te dibu­jos tra­cen la tra­yec­to­ria del reco­rri­do de un auto­mó­vil. Para­le­la­men­te a estos con­cep­tos pro­yec­ti­vos, los con­cep­tos topo­ló­gi­cos, se trans­for­ma­rán tam­bién, en con­cep­tos eucli­dia­nos. Comen­za­rán a per­ci­bir los obje­tos de su espa­cio exte­rior, no como algo está­ti­co sino con movi­mien­to.  Que cons­tru­yan maque­tas sepa­ran­do zonas con plas­ti­li­nas, como su casa de la escue­la. Median­te este tipo de ejer­ci­cio podrán com­pren­der que un cuer­po rígi­do al tener una trans­for­ma­ción, de movi­mien­to de rota­ción o de tras­la­da­ción, con­ser­va las pro­pie­da­des de lon­gi­tud, ángu­los, áreas y volú­me­nes. Y que des­ta­quen la pre­sen­cia de hue­cos o zonas y las líneas fron­te­ra que limi­tan diver­sas figu­ras.

En cada tarea se esta­ble­ce­rán ejes de pre­gun­tas abier­tas res­pec­ti­va­men­te. Estos con­jun­tos de ejer­ci­cios los podrán poner en prác­ti­ca, igual­men­te, con base en algu­nas de las acti­vi­da­des seña­la­das en la figu­ra 1–4.

En resu­men, éstas serían algu­nas de las acti­vi­da­des bási­cas con las que podrían ser entre­na­dos los niños pre­es­co­la­res y esco­la­res en cuan­to al desa­rro­llo de la noción de espa­cio, en su geo­me­trías topo­ló­gi­ca, pro­yec­ti­va y eucli­dia­na, en el salón de cla­se; apo­yán­do­se el docen­te en el mane­jo de algu­nos de estos ejer­ci­cios prác­ti­cos u otros com­ple­men­ta­rios, seña­la­dos en las figu­ras 1–4 con sus res­pec­ti­vas varia­cio­nes y ano­ta­dos en esta pro­pues­ta de tra­ba­jo didác­ti­co, con orien­ta­ción psi­co­ge­né­ti­ca.

REFRENCIAS

Notas